de diagonaal van een parallelogram, volkomen dezelfde uitwerking heeft als twee krachten te zamen, die elke volgens eene der twee zijden van het parallelogram werken, welke hetzelfde hoekpunt met de diagonaal gemeen hebbe; wanneer slechts alle drie krachten in denzelfden zin werken en de lengte der genoemde lijnen zelve hare maat voorstelt. Men zegt dan, dat de kracht volgens de diagonaal ontbonden is in de beide krachten volgens de zijden: en omgekeerd, dat beide laatste krachten zijn te zamen gesteld tot de kracht volgens de diagonaal, hare resultante: en dit alles zoowel in rigting als in grootte.
Raakt dus de handbal den speelbal in eene rigting AH, (Fig. 1.)
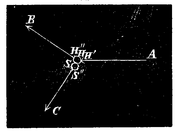
Fig. 1.

Fig. 2.
schuins staande op de verbindingslijn der middelpunten HS (bij eenen zoogenaamden schuinschen stoot), zoo kan men voor de snelheid van den handbal of liever voor de kracht HA (Fig. 2), die daarvan als oorzaak wordt aangenomen, twee andere krachten HB en HC, in de plaats stellen, waarvan de eene HC gerigt is volgens die verbindingslijn, de andere HB volgens eene lijn, die de beide ballen in hun raakpunt aanraakt. De laatste kracht HB zal slechts te weeg brengen, dat de handbal zich in die rigting na den schok voortbeweegt, en zal op den schok geenen invloed uitoefenen. Anders is het met de eerste kracht HC, die eigenlijk alleen den schok te weeg brengt: op deze blijft het vroeger gezegde volkomen toepasselijk. Nemen wij voortaan, daar wij ons toch met benaderde uitkomsten hier moeten tevreden stellen, de ballen als volkomen veerkrachtig aan, dan verliest de handbal alle snelheid volgens de rigting der lijn, die de middelpunten vereenigt, en deze snelheid gaat geheel op den speelbal over. Na den schok dus verkrijgen de speelbal en de handbal bewegingen, waarvan snelheid en rigting (Fig. 1) worden voorgesteld door de ontbondenen van de

