Album der Natuur/1854/Gewigt Aardbol, Grothe
| Het Gewigt van den Aardbol (1854) door Peter Dietrich Grothe |
| 'Het Gewigt van den Aardbol' werd gepubliceerd in Album der Natuur (derde jaargang (1854), pp. 185–193. Dit werk is in het publieke domein. |
"Is het gewigt des aardbols te bepalen? Wie heeft ooit de aarde op eene weegschaal gelegd? Ik voor mij houd het voor onmogelijk zulk een moeijelijk vraagstuk op te lossen." Zoo zal waarschijnlijk meer dan een lezer van het Album der Natuur spreken, vooral hij, die in de natuur- en werktuigkunde geene grondige kundigheden heeft kunnen verzamelen. Echter is het met dit onderwerp als met vele anderen. Vertelt gij aan eenen onkundigen, dat men den afstand der zon van de aarde vrij naauwkeurig op 20½ millioenen geographische mijlen of ruim 26 millioen uren gaans heeft berekend, dan zal hij u ronduit verklaren, dat zoodanige berekeningen niet uit te voeren zijn. Eene zonsverduistering te berekenen en de plaatsen op de aarde aan te wijzen, waarop bij dit verschijnsel de schaduw der maan moet vallen, is inderdaad een niet gemakkelijk vraagstuk, en voor allen, die geen begrip hebben van de verbazende magt der wiskundige wetenschappen, schijnbaar onoplosbaar. En toch heeft de ondervinding voor twee jaren ons weder moeten overtuigen, dat de sterrekundigen deze berekening met eene groote juistheid weten uit te voeren. Nog een zeer merkwaardig voorbeeld. De Fransche sterrekundige leverrier, besloot uit zekere, naauwelijks waarneembare verschijnselen der planeet Uranus, dat er nog dieper in de oneindige ruimte, en wel op meer dan 600 millioen uren gaans van de zon, eene tot dusverre onbekend gebleven planeet moest bestaan. Hij berekende deze verschijnselen, en bepaalde op den verbazend grooten afstand van 1000 millioenen uren de kleine plek aan den hemel, waar men op eenen zekeren tijd met goede verrekijkers de planeet moest kunnen zien. En dat die berekening nagenoeg geheel juist [ 186 ]was bleek, want leverrier deelde zijne uitkomsten mede aan den sterrekundige galle te Berlijn, en op den avond van denzelfden dag was het onbekende hemelligchaam reeds gevonden.
Deze voorbeelden kunnen bewijzen, tot welke verbazende hoogte de geest van den mensch zich kan ontwikkelen, indien men, door goed onderwijs voorbereid, zijne studiën met ijver voortzet en dan met standvastigheid en volharding een gesteld doel tracht te bereiken. Doch niet alleen de plek aan den hemel, waar de nieuwe planeet zich moest bevinden, werd door die berekening aangewezen; ook haar gewigt volgde onmiddellijk daaruit. Wie zal zich thans nog verwonderen, wanneer beweerd wordt, dat het gewigt des aardbols berekend en betrekkelijk vrij naauwkeurig berekend is? Ook is de wijze hoe dit geschiedt geenszins zeer ingewikkeld en moeijelijk te begrijpen; integendeel, ze is zoo eenvoudig dat een ieder er zich gemakkelijk mede kan bekend maken. Wij hebben daarom ook gemeend, dat dit onderwerp bij vele lezers belangstelling zoude opwekken, en zullen dus trachten, op de volgende bladzijden zoo eenvoudig mogelijk de wijze der bepaling van het gewigt des aardbols te ontvouwen.
Alvorens wij echter daarmede aanvangen, moeten wij eerst op een zeer eenvoudig natuurverschijnsel opmerkzaam maken, dat wel algemeen bekend is, maar toch zelden met oplettendheid wordt gade geslagen. Dit verschijnsel bestaat in het streven van alle ligchamen, zonder uitzondering, om zich naar elkander toe te bewegen; een bewijs dat zij, zoo als men dit doorgaans uitdrukt, elkander aantrekken. Dat alle ligchamen door onzen aardbol aangetrokken worden, bemerken wij ieder oogenblik, want juist deze aantrekking doet ze zich naar de aarde toe bewegen, zoodra zij daarin niet verhinderd worden; juist deze aantrekking maakt ze zwaar. Om echter de aantrekking zigtbaar te maken, die twee kleine ligchamen, welke op eenigen afstand van elkaar geplaatst zijn, op elkander uitoefenen, dit is niet gemakkelijk en vereischt fijne en naauwkeurige werktuigen. Maar zoodanige proeven zijn eigenlijk overtollig. Ziet gij niet de waterdeeltjes der droppels zamenhangen; insgelijks de droppels zelve aan de boomtakken en bladen? Neemt [ 187 ]gij niet waar, dat uwe hand nat wordt als gij ze in het water dompelt? Stijgt niet de thee in een stuk suiker, de inkt in de pen, de olie in de lampenkousen op? En waarom dat? Omdat deze vloeistoffen door de ligchamen waarmede zij in aanraking zijn gebragt, aangetrokken worden. Maar de natuurkundigen, die hunne wetenschap op eenen vasten grondslag moeten opbouwen, hebben zich met zoodanige proeven niet kunnen vergenoegen, en derhalve met de fijnste en best bewerkte toestellen, onder inachtneming der grootste zorg en naauwkeurigheid, nog andere proeven dienaangaande gedaan, en daarbij steeds de stelling bewaarheid gevonden, dat alle ligchamen elkander aantrekken.
Bij de genoemde naauwkeurige proeven heeft men echter nog meer opgemerkt. In de eerste plaats vertoonde zich de aantrekkende werking des te grooter, naar gelang het aantrekkende ligchaam een grooter gewigt bezat, zoodat dus een bol van twee ponden ook juist eene tweemaal zoo groote aantrekking uitoefende als eene andere bol van één pond. De stof, waaruit het aantrekkend ligchaam bestaat, heeft daarbij hoegenaamd geen invloed, en twee bollen van hetzelfde gewigt, de eene van lood, de andere van ijzer, hebben in dit opzigt gelijke werking. Deze door de ervaring vastgestelde wet drukken wij op de volgende wijze in woorden uit:
De aantrekkingskrachten van twee ligchamen op gelijke afstanden van het aangetrokken ligchaam staan in dezelfde verhouding (in regte reden) als hunne gewigten.
Ten tweede zag men de aantrekkingskracht verminderen, wanneer men het aantrekkend ligchaam verwijderde, zoo als ook moest verwacht worden; want altijd zal de invloed, van welken aard ook, dien het eene op het andere uitoefent, met de vermeerdering van den afstand minder worden. Men zoude nu wel vermeenen, dat op den dubbelen afstand de aantrekkingskracht tweemaal kleiner, dus de helft, en op den drie- en viervoudigen afstand, slechts een derde en een vierde gedeelte van de vroegere, op den enkelen afstand bestaande aantrekkingskracht moest zijn. Maar uit de proeven is dit niet gebleken; men moest veeleer daaruit besluiten, dat de aantrekkende werking met de vermeerdering van den afstand eene [ 188 ]betrekkelijk grootere vermindering ondergaat, daar op den dubbelen, drie- en viervoudigen afstand de aantrekkingskracht niet meer bedraagt dan 1⁄4, 1⁄9, 1⁄16 van de vroegere; en deze getallen zijn de tweede magten of vierkanten van 1⁄2, 1⁄3, 1⁄4 die wij hadden verwacht. Deze verhouding was ook reeds veel vroeger, door den vermaarden Engelschen wiskundige i. newton, uit verschijnselen aan den sterrenhemel afgeleid. Deze tweede wet luidt derhalve:
De aantrekkingskracht eens ligchaams op een ander vermindert in reden als de tweede magt des afstands vermeerdert.
Thans zijn wij uitgerust, om tot de oplossing van het gestelde vraagstuk te kunnen overgaan. Wij houden ons nu overtuigd, dat een looden bol of elk ander willekeurig ligchaam op de oppervlakte der aarde, waar ook gelegen, aangetrokken wordt, en wel van alle deelen der aarde, echter niet van allen even sterk. Ten gevolge dezer aantrekkingskracht van alle deelen der aarde, valt de looden bol naar den grond, indien men hem niet ondersteunt, of hij drukt op een ander ligchaam, waarop hij rust, dat is te zeggen, hij bezit een gewigt, of hij spant eene koord of draad wanneer hij daaraan is opgehangen. Op de laatste wijze verkrijgt men het zoogenaamde schietlood, een schijnbaar nietig maar zeer gewigtig werktuigje, hetwelk op de gemakkelijkste wijze ons de lijn aanwijst, waarin de aantrekkingskracht der aarde werkt en de ligchamen trachten te vallen. Deze rigting is loodregt op de horizontale of waterpasse vlakte, die voor elke plaats door den spiegel eener rustende vloeistof wordt aangewezen, en, in zoover als de aarde als bolvormig mag beschouwd worden, gaat de lijn, door den draad van het schietlood bepaald, verlengd zijnde, door het middelpunt der aarde. Eene zeer onbeduidende afwijking heeft plaats op alle plaatsen tusschen den evenaar en de polen, uithoofde dat de aarde aan de polen afgeplat is en tevens omwentelt.
Eene soortgelijke afwijking van de loodlijn moet ook plaats hebben, wanneer in de nabijheid van het schietlood, bezijden de loodlijn, aan den eenen kant meer aantrekkende stofdeelen zijn opgehoopt, die eene wijziging der gezamenlijke aantrekkingskracht moeten teweeg brengen. Onderstellen wij namelijk, dat in eene [ 189 ]vlakke streek, ver van bergen en andere verheven voorwerpen, een schietlood vrij naar beneden hangt, dan zal de draad regthoekig, dat is, loodregt zijn op den horizon, of ten naastenbij in de rigting naar het middelpunt der aarde. Wat zoude er nu gebeuren, indien er op eens eene aanzienlijke bergmassa in deze streek, niet te ver van het schietlood verwijderd, uit den grond oprees, zoo als zulks in vulkanische landen somtijds werkelijk geschiedt? Uit de straks genoemde wetten der aantrekkingskracht volgt noodwendig, dat de bol van het schietlood meer of min in de rigting naar dezen berg toe zich zoude bewegen, en wel des te meer, naar gelang dat de berg meer weegt of de afstand minder wordt. Door deze beweging des bols naar den berg toe, komt echter het koord waaraan de bol hangt, uit de loodregte rigting, met andere woorden, het hangt niet meer loodregt, maar schuinshellende naar den opgerezen berg. En juist hetzelfde verschijnsel moet zich voordoen, wanneer men opzettelijke proeven doet met een schietlood, in de nabijheid van reeds bestaande bergkegels. Men zal daarvan nog een duidelijker denkbeeld verkrijgen door de beschouwing der bijgevoegde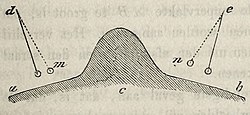 figuur, waarin a b een gedeelte der oppervlakte van de bolvormige aarde voorstelt, op hetwelk een meer of minder aanzienlijke berg c rust. Bestond die berg niet, was dus de grond effen in de rigting der kromme vlakte a b, dan zouden schietlooden, in de punten d en e opgehangen, de loodregte rigting aannemen en de draden zouden verlengd in het middelpunt der aarde elkander ontmoeten. Maar door de inwerking van den berg c moet het schietlood in d eene rigting verkrijgen zoo als d m, terwijl het in e geplaatste die van de lijn e n aanneemt. Wij vermeenen, dat dit duidelijk genoeg is, om geene verdere toelichting te behoeven. Zien wij nu, of men in staat is, deze afwijking te bepalen en of men daardoor tot die uitkomst kan geraken, welke men verlangt.
figuur, waarin a b een gedeelte der oppervlakte van de bolvormige aarde voorstelt, op hetwelk een meer of minder aanzienlijke berg c rust. Bestond die berg niet, was dus de grond effen in de rigting der kromme vlakte a b, dan zouden schietlooden, in de punten d en e opgehangen, de loodregte rigting aannemen en de draden zouden verlengd in het middelpunt der aarde elkander ontmoeten. Maar door de inwerking van den berg c moet het schietlood in d eene rigting verkrijgen zoo als d m, terwijl het in e geplaatste die van de lijn e n aanneemt. Wij vermeenen, dat dit duidelijk genoeg is, om geene verdere toelichting te behoeven. Zien wij nu, of men in staat is, deze afwijking te bepalen en of men daardoor tot die uitkomst kan geraken, welke men verlangt.
Veronderstellen wij een zoo klein gedeelte van den aardbodem, [ 190 ]dat het als een plat vlak kan beschouwd worden, zoo als A B in figuur 2, 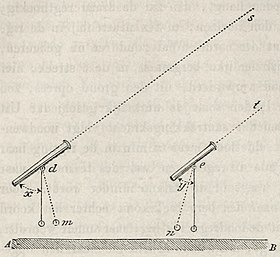 dan zijn de rigtingen van het schietlood in d en e beiden loodregt op dit vlak en derhalve onderling evenwijdig. Nemen wij aan, dat in de punten d en e twee verrekijkers zijn geplaatst en beiden gerigt op eene en dezelfde vaste ster, dan zal wegens den verbazende afstand der vaste ster, ook de as van den eenen verrekijker evenwijdig moeten zijn met de as van den anderen kijker, of de lijn d's evenwijdig aan e t. Hieruit volgt nu, dat het schietlood in de beide plaatsen met de verrekijkers twee hoeken x en y vormt, die onderling gelijk zijn. Deze gelijkheid heeft echter niet meer plaats, indien de oppervlakte A B te groot is, om nog als een plat vlak te kunnen worden aangezien. Het verschil dat bestaat, laat zich intusschen uit den afstand d e en den straal des aardbols gemakkelijk berekenen.
dan zijn de rigtingen van het schietlood in d en e beiden loodregt op dit vlak en derhalve onderling evenwijdig. Nemen wij aan, dat in de punten d en e twee verrekijkers zijn geplaatst en beiden gerigt op eene en dezelfde vaste ster, dan zal wegens den verbazende afstand der vaste ster, ook de as van den eenen verrekijker evenwijdig moeten zijn met de as van den anderen kijker, of de lijn d's evenwijdig aan e t. Hieruit volgt nu, dat het schietlood in de beide plaatsen met de verrekijkers twee hoeken x en y vormt, die onderling gelijk zijn. Deze gelijkheid heeft echter niet meer plaats, indien de oppervlakte A B te groot is, om nog als een plat vlak te kunnen worden aangezien. Het verschil dat bestaat, laat zich intusschen uit den afstand d e en den straal des aardbols gemakkelijk berekenen.
Nemen wij thans het eenvoudigste geval aan, dat is, dat de hoeken x y gelijk zijn, en verbeelden wij ons vervolgens, dat er tusschen de beide kijkers in d en e de berg c der figuur 1 geplaatst wordt. Het schietlood in d verkrijgt dan de rigting d m en dat in e de rigting e n. Men zal aanstonds zien, dat dan de hoek x grooter en de hoek y kleiner moet worden. Bevindt zich bovendien de berg juist in het midden van d en e, dan zullen ook de beide afwijkingen van de loodlijnen gelijk zijn, en deze afwijking zal klaarblijkelijk gelijk zijn aan het halve verschil der beide hoeken, die nu door de draden der schietlooden met de as van de verrekijkers gevormd worden.
Dit is de manier, om na te gaan, of er eene afwijking van het schietlood in de nabijheid van enkele bergtoppen bestaat en hoe[ 191 ]veel die bedraagt. Zij is het eerst in toepassing gebragt door den Engelschen sterrekundige maskelyne, die daaromtrent proeven deed in de nabijheid van den bergketen Shehallien in Schotland, een gebergte, dat zich van het westen naar het oosten uitbreidt, zoo dat hij, om de afwijking waar te nemen, zijne toestellen ten noorden en ten zuiden moest opstellen.
Nadat door zoodanige proeven de schuinsche rigting van het schietlood bewezen is, moet verder onderzocht worden, waardoor die is voortgebragt. Uit de bovengenoemde grondwetten volgt, dat alle enkele deelen, waaruit de berg bestaat, daartoe medewerken; maar daar toch de bol van het schietlood niet aan de werking van elk deeltje in het bijzonder kan voldoen, zoo zal er een punt in den berg bestaan, dat als de plaatsvervanger van alle overige kan gelden, en in welks rigting de bol zich dan moet bewegen. Dit punt is het middelpunt, of beter, het zwaartepunt van den geheelen berg. Wanneer men dan door naauwkeurige opmetingen van den berg deszelfs inhoud heeft bepaald, dan zal men, onder inachtneming van den aard en het soortelijke gewigt der rotssoorten, waaruit de berg is zamengesteld, eensdeels dit zwaartepunt en anderdeels ook het eigenlijke gewigt in willekeurige eenheden, b.v. Nederlandsche ponden, kunnen uitdrukken. Door deze, wel is waar vrij omslagtige en moeijelijke bepalingen, leert men dus de hoegrootheid kennen zoowel van den afstand van het aantrekkende zwaartepunt tot aan het schietlood, als van het gewigt van het aantrekkende ligchaam of den berg, welke beide gegevens noodig zijn ter bepaling van de hoegrootheid der aantrekkingskracht, die de berg uitoefent.
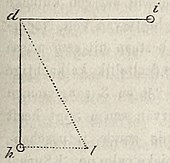 Maar daarenboven is nog iets te bepalen, en dit is ook het laatste. Hangt het schietlood in het punt d fig. 3, en is het alleen onderworpen aan de zwaartekracht der aarde, dan zoude het de loodregte rigting d h aannemen. Bezat de aarde geene aantrekkingskracht, en was de bol van het werktuig slechts onderhevig aan de aantrekking des [ 192 ]bergs, dan moest de draad in de rigting naar het zwaartepunt van den berg, nagenoeg horizontaal, dus in de lijn d i komen, wanneer de berg aan de regterzijde van de figuur ondersteld wordt te zijn. Door de vereenigde werking beider krachten, neemt de draad de schuinsche rigting d l aan. Uit de eerste wetten der werktuigkunde volgt, dat, indien men de lijn h l evenwijdig aan de lijn d i trekt, de verhouding der lijnen d h en h l ook de verhouding der beide straks genoemde krachten uitdrukt. Deze verhouding van h l tot d h wordt echter zeer gemakkelijk uit den afwijkingshoek h d l berekend, die door de boven opgestelde handelwijze gevonden is. Wij maken hieruit op, dat de aantrekkingskracht des bergs zich verhoudt tot de geheele zwaartekracht als de bekende lijnen h l en d h. Maar beide krachten staan nog tot elkander in de zamengestelde reden van, ten eerste, het gewigt des bergs tot het gewigt der aarde; en ten tweede omgekeerd, als de afstand van het zwaartepunt des bergs en de afstand van het middelpunt der aarde tot aan het schietlood. In deze eenvoudige evenredigheid, welker oplossing op een gemakkelijk vraagstuk des regels van drieën nederkomt, is alles gegeven, behalve het gewigt der aarde, hetgeen daaruit wordt gevonden.
Maar daarenboven is nog iets te bepalen, en dit is ook het laatste. Hangt het schietlood in het punt d fig. 3, en is het alleen onderworpen aan de zwaartekracht der aarde, dan zoude het de loodregte rigting d h aannemen. Bezat de aarde geene aantrekkingskracht, en was de bol van het werktuig slechts onderhevig aan de aantrekking des [ 192 ]bergs, dan moest de draad in de rigting naar het zwaartepunt van den berg, nagenoeg horizontaal, dus in de lijn d i komen, wanneer de berg aan de regterzijde van de figuur ondersteld wordt te zijn. Door de vereenigde werking beider krachten, neemt de draad de schuinsche rigting d l aan. Uit de eerste wetten der werktuigkunde volgt, dat, indien men de lijn h l evenwijdig aan de lijn d i trekt, de verhouding der lijnen d h en h l ook de verhouding der beide straks genoemde krachten uitdrukt. Deze verhouding van h l tot d h wordt echter zeer gemakkelijk uit den afwijkingshoek h d l berekend, die door de boven opgestelde handelwijze gevonden is. Wij maken hieruit op, dat de aantrekkingskracht des bergs zich verhoudt tot de geheele zwaartekracht als de bekende lijnen h l en d h. Maar beide krachten staan nog tot elkander in de zamengestelde reden van, ten eerste, het gewigt des bergs tot het gewigt der aarde; en ten tweede omgekeerd, als de afstand van het zwaartepunt des bergs en de afstand van het middelpunt der aarde tot aan het schietlood. In deze eenvoudige evenredigheid, welker oplossing op een gemakkelijk vraagstuk des regels van drieën nederkomt, is alles gegeven, behalve het gewigt der aarde, hetgeen daaruit wordt gevonden.
Deelen wij ten slotte nog mede, wat de uitkomsten zijn geweest van deze moeijelijke proeven, gedaan door maskelyne in de jaren van 1774 tot 1776. Alle omstandigheden naauwkeurig in aanmerking genomen, in welker bijzonderheden wij hier niet willen treden, berekende men uit de verkregen uitkomsten, dat de geheele aarde gemiddeld 1,8 maal zwaarder moest zijn, dan een even groote inhoud van de rotsmassa, waaruit de berg bestaat. Wij zullen dit nog trachten duidelijker te maken. Het is bekend dat een kubieke palm of eene kan zuiver water een gewigt heeft van één Nederlandsch pond. De rotsen van den Shehallien bestaan uit eene massa van gedeeltelijk basalt- en syenietachtige, gedeeltelijk kalkachtige gesteenten, wier soortelijk gewigt tusschen 2¾ en 3 aangenomen kan worden, zoodat een kubieke palm daarvan een gewigt heeft van 2¾ tot 3 ponden. Van de geheele aarde zoude intusschen, volgens de proeven en berekeningen, elke kubieke palm nog 1,8 maal [ 193 ]zwaarder moeten zijn, dat is, elke kubieke palm zoude gemiddeld een gewigt hebben van 4,95 tot 5,4 ponden, en hieruit zoude het soortelijk gewigt der aarde gemiddeld ten naastenbij 5 moeten zijn.
Later heeft men door de inrigting van zeer naauwkeurige toestellen, waarbij in de plaats van een berg andere kleine ligchamen worden gebezigd, om de hoegrootheid der daardoor teweeg gebragte afwijkingen te meten, deze waarnemingen veel eenvoudiger en zekerder gemaakt. Eene uitvoerige beschrijving dier toestellen zoude hier echter misplaatst zijn. Ook willen wij hier nog ter loops gewagen van eene andere handelwijze, namelijk die, om door slingerproeven het soortelijk gewigt of de digtheid der aarde te bepalen. Men zal ligtelijk begrijpen, dat, indien de schommelingen des slingers worden voortgebragt door de zwaartekracht der aarde, de snelheid dier schommelingen moet vermeerderen, indien men den slinger plaatst op een verheven, vrij sterk aantrekkend ligchaam, b.v. op den top van eenen bergkegel, eene der Egyptische piramiden enz.; waarbij in aanmerking moet worden genomen, dat men gelijktijdig eene vermindering der snelheid zal hebben, omdat men verder van het middelpunt der aarde verwijderd is. Wij geven hier alleen de uitkomsten die men op de genoemde beide wegen heeft verkregen.
De proeven, die carlini op den Mont Cenis in de Savooische Alpen met den slinger heeft genomen, leverden voor de aarde een soortelijk gewigt van 4,39. De Engelschman cavendish liet aan eene Coulombsche wringingsbalans een klein ligchaam onder den invloed van eenen zwaren bol schommelen en berekende daaruit het soortelijke gewigt 5,48. Eene reeks van meer dan 2000 proeven met zeer verschillende stoffen en met denzelfden toestel door baily voor omtrent 20 jaren gedaan, heeft daarentegen 5,67 opgeleverd. Welk van deze getallen van 4,39 tot 5,67 het naast met de waarheid overeenkomt, is nog niet te beslissen; maar men ziet, de grens is nog al vrij naauw. Nemen wij het gemiddelde of het getal 5, dan weegt elke kubieke el der aarde 5000 Nederlandsche ponden, derhalve, daar de omtrek 40 millioenen ellen is, de geheele aarde niet minder dan 5 401600 000000 000000 000000 Nederlandsche ponden.
