Wandelen en Waarnemen/2

Wandelen en waarnemen : schetsen uit het leven van planten en dieren (1906) door Eli Heimans

Uitgegeven in Amsterdam door Van Holkema en Warendorf.

[ 15 ]

II.

Het geheim van de rozen.

In Juni is het de volle mooie rozentijd. In de duinen, in de parken en in de tuinen, aan den zuidzoom van de bosschen en in de hagen langs de roggevelden, overal en overal bloeien de rozen, wilde en gekweekte, prachtige centifolia's en eenvoudige, even mooie enkele; hoogstammen en maandrozen, zacht, zoet of bedwelmend van geur; gloeiend van kleur of teer van tint en zoo exquis van vorm, dat het aanraken met onze grove vingers een zonde tegen de schoonheid lijkt.

Of ze als lage duinroosjes onze heuvels met een wit en groen rozentapijt beleggen, of als klimrozen villagevels en kerkmuren draperen, altijd weten ze ieders oog te bekooren door een volmaakte schoonheid. De meeste bloemen zijn aan de mode onderhevig, hebben tijden van eer en van vergetelheid; de roos is de klassieke bloem; de bloem die al in oude tijden door Grieken, Gothen en Romeinen gekweekt en bezongen werd; later, vooral in Midden-Europa ontstond een ware vereering, een rozencultus.

Is het te verwonderen dat het een wonderbloem werd, een remedie tegen alle kwalen, een talisman tegen het ongeluk, een toovermiddel tegen het booze oog, het symbool der liefde bij uitnemendheid, de bloem van fabel en mythe?

Maar bovendien is er sedert onheugelijke tijden iets geheimzinnigs in het rozensymbool ontstaan. Het was bij de Grieken [ 16 ]de bloem van Venus en in een oude mythe wordt al gewaagd van haar zoon Eros (de dageraad) die de roos van Venus aan Harpokrates schonk, opdat geheim zou blijven wat zijn moeder misschien verkeerds had gedaan.

Zoo ook schilderde de waard een roos aan de zoldering boven de stamtafel, en wat daar onder dit teeken, sub rosa, van elkaar of van anderen verteld werd, mocht geen oningewijde ter oore komen.

Over het geheim van den rozenknop zijn in de middeleeuwen allerlei verhalen in omloop gekomen: de bloembladeren die elkaar zoo wonderlijk mooi omsluiten, de plooien van de binnenste bladeren, de stand van stempels en meeldraden, dat alles had een bijzondere geheime beteekenis, die met het lot van den mensch in verband stond.

De beroemde Albertus Magnus vond in de 13de eeuw nu ook nog een uiterlijk geheim aan de rozenkelk. Deze slippen namelijk hebben de eigenaardigheid ongelijk en toch regelmatig te zijn.

leder kan bij de meeste rozensoorten (tenzij het door voortgezette kweeking zeer gewijzigde hybriden zijn geworden) die vreemde kelkvorming terugvinden. Let maar op de randen van de vijf slippen. Twee zijn er die zijslipjes hebben, soms vele en lange, alsof elke slip een diep ingesneden rozenblaadje was, twee zijn geheel gaaf van rand; één is kaal aan de eene zijde, met slipjes voorzien, maar "gebaard" aan de andere zijde.

Wie dit gezien heeft, kent ook de oplossing van het oude Latijnsche rozenraadsel:

Quinque sunt fratres;
Duo sunt barbati;
Duo sine barba nati;
Unus e quinque
Non habet barbam utrinque.

[ 17 ]

Rozeknoppen van verschillende zijden gezien, om de gebaarde en baardelooze kelkslippen en de halfgebaarde naar voren te brengen.

Wat zeggen wil: Er waren eens 5 broeders; twee kregen een baard, twee zijn zonder baard gebleven, en een droeg aan ééne zijde een baard.

Dit is op zichzelf al iets bijzonders; maar geheimzinniger wordt de zaak als men de rozenkelk recht voor zich houdt en op de volgorde van de verschillende slippen let.

De twee broeders met baarden staan niet naast elkaar; en de twee baardelooze ook niet; de half geschoren heer is tusschen de kaalste en de harigste broer geplaatst.

[ 18 ]Telt ge van de slip met de zwaarste baard naar de tweede baard, dan naar de halve en eindelijk naar de baardelooze, dan moet ge telkens een slip overslaan. Gaat ge van 1 tot 5 in tegengestelde richting, dan moet ge twee overslaan om de volgorde der baarden te krijgen. Teeken de kelk even op een papier, zet 5 nummers bij de slippen in de volgorde der baarden, en trek nu zonder het potlood op te lichten van 1 over 2, 3 en 4 naar vijf, dan hebt ge het geheimzinnige figuur, de overoude hieroglyphe, het teeken dat in de middeleeuwen een huivering kostte aan ieder die het toevallig bij één of ander ding opmerkte, het pentagram of de drudenvoet, het oude symbool van het raadselachtige en het verborgene, dat op de mantels der priesters, op de brieven der philosofen uit de school van Pythagoras voorkomt.

Ook op oude zegelringen uit het oosten is het gevonden en later werd het wel als vensterroos in Gothische kerken gezet; zelfs den duivel was dat teeken te machtig; denk maar aan Mephisto, die niet over den drempel van Faust's studeervertrek kon komen.

En zie, dezelfde groote geest, dezelfde Goethe, die Faust en Mephistofeles schiep, ontdekte het geheim van het pentagram in de rozenkelk. Hij was het die in de botanische wetenschap de theorie van de metamorphose der bladeren invoerde: alle bloemdeelen, ook kroon- en kelkbladeren zijn niet anders dan vervormde stengelbladeren.

Die rozenkelkslippen zijn bladeren, die hoe meer ze de bloem naderen, sterker van gewone bladeren afwijken. En nu behoeft ge maar even den stand van de stengelbladen bij een roos na te gaan om in de raadselachtige rozenkelk een bewijs voor Goethe's stelling te vinden.

Daartoe moet ge een heel lange, jonge, recht opgeschoten [ 19 ]loot nemen, die geen wringing of draaing vertoont; bij in 't volle licht opgeschoten struiken komt ge het beste klaar.

Wind bij den voet van zoo'n samengesteld blad een dun wit draadje om den stengel, en slinger het onder langs de voeten van de daarboven geplaatste bladeren, zóó dat ge dus de plaatsen raakt, waar het rozenblad (dat bestaat meest uit 7 of 9 blaadjes aan één steel) uit den stengel komt. Nu ziet ge dadelijk dat het zesde blad net weer boven het eerste komt te staan, het zevende boven het tweede, enz. Ook merkt ge, dat ge tweemaal den stengel rond zijt geweest, vóór het zesde blad kwam, ge hebt een spiraal met twee windingen om den rozenstengel geslagen.

De vijf bladeren zijn dus spiraalsgewijze om den stengel geplaatst, zóó dat vijf bladeren op twee windingen komen. Denkt ge u nu, terwijl ge den tak met het draadje in de hand hebt de loodrechte afstanden tusschen elke twee bladeren wat korter, nog wat korter, dan komen de bladeren op 't laatst in een kring te staan, met de voeten dus ongeveer op één hoogte. En kijk nu maar na (maar nummer eerst even de bladeren van onder naar boven) het tweede blad, dat ge in gedachten hebt laten zakken, komt nu niet naast het eerste te liggen, want het hooger geplaatste No. 4 van de tweede winding valt er tusschen, zoo No. 5 tusschen 3 en No. 1.

De rozekelkslippen zijn op dezelfde wijze geplaatst, vijf op twee spiralen, die plat zijn gedrukt zoodat de vijf blaadjes naast elkaar kwamen te liggen. Zoo is al het angstig geheimzinnige van het rozenpentagram weggeblazen, door de kalm voortschrijdende wetenschap.

Als het op een Zondag regent, moet u met de kinderen het zaakje maar eens uitzoeken; het niet opgeven als het niet dadelijk lukt; het kòmt uit.

[ 20 ] En heeft u er al hoogere burgers of gymnasiasten bij, zoek dan ook den bladstand bij andere planten te bepalen; met heesters gaat dat het beste.

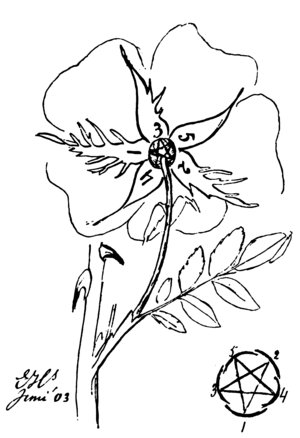
Een rozenkelk, vlak uitgespreid, van onder gezien.
Onderaan het pentagram.

In de botanie drukt men dien stand in cijfers uit. De rozenbladstand is ²⁄₅, d.w.z., zooals ge nu al weet: vijf bladeren op twee spiraalwindingen, het 6^de boven het eerste. Deze stand komt zeer veel voor. Andere zijn: ¹⁄₂, ¹⁄₃, ²⁄₅, ³⁄₈, ⁵⁄₁₃,⁸⁄₂₁, ¹³⁄₃₄, ²¹⁄₅₅,³⁴⁄₅₉. De voorste komen bij eenzaadlobbige planten (leliesoorten o.a.) veel voor, ³⁄₈, en de hoogere cijfers bij planten met bladrozetten, zooals huislook.

Schimper en Braun hebben die bladstandgeschiedenis uitvoerig onderzocht.

[ 21 ]Als er geen zetfout in de cijfers sluipt, zullen de wiskunstenaars onder de jongelui, wel het regelmatige in deze breuken laten opmerken. Elke volgende teller en noemer is namelijk gelijk aan de som van de beide vorige; zoodat de getallen die de tellers voorstellen, 1, 2, 3, 5, 8 enz., een in de wiskunde bekende betrekking aangeven, af te leiden uit een kettingbreuk, met z = 2.

Zoo is pas het raadsel van den stokouden Albertus Magnus ontsluierd, of daar komen een paar splinternieuwe botanici weer een geheimzinnige mathematica in den bouw van de plant ontdekken, die nog veel wonderlijker is.