Album der Natuur/1858/Het billard
| Iets over het billard (1858) door David Bierens de Haan |
| 'Iets over het billard' werd gepubliceerd in Album der Natuur (zevende jaargang (1858), pp. 65-92. Dit werk is in het publieke domein. |
Het toepassen van de grootsche wetten der natuur tot nut der menschheid is de opgave dezer eeuw: niet minder belangrijk is die toepassing tot ons gemak en ons genoegen. Onze spelen komen te rade bij de kansrekening en bij de leer der combinatiën, bij de meetkunde van ligging of bij de leer der beweging: maar juist daardoor ook, zoo als genoeg bekend is, hebben zij die wetenschappen zelve doen ontwikkelen. Zoo is het knikkeren, het kolf- en het billardspel op de leer der botsing gegrond, en wel het laatste onder de meest gunstige omstandigheden; bij eene beschouwing daarvan zullen wij natuurverschijnselen, die anders vrij zamengesteld zijn in hunnen oorsprong, zich zien ontwikkelen in ons bekende vormen. De oorzaken van den verschillenden loop der ballen na te gaan, zoowel als de leer der wrijving en der botsing op dien loop toe te passen en deze uitkomsten aan de ondervinding te toetsen,—ziedaar een onderwerp, dat zeker in dit tijdschrift niet misplaatst is, en belangrijke uitkomsten kan opleveren, ook zonder in hoogere wetenschappelijke bespiegelingen te vervallen.
Het is hier niet noodig, eene lofrede op het billardspel te houden: alleen zij opgemerkt, dat het geacht wordt voor het ligchaam eene even nuttige en edele uitspanning en inspanning te zijn, als het schaakspel voor den geest: vandaar dat beide tot de edele spelen worden gerekend. Het billardspel, naar het schijnt ongeveer drie eeuwen oud, is vooral van aard veranderd, sedert mingaud den top der Queue met een stukje leder of kurk voorzag, en daardoor den excentrischen stoot invoerde, waardoor alleen het mogelijk werd, aan den bal die bijzondere bewegingen mede te deelen, welke aan dit spel juist het [ 66 ]eigenaardige belang bijzetten. En het is dan ook eerst door deze verbetering, dat de beschouwing van het billardspel van meer bijzonder wetenschappelijk belang is geworden, door den speler in de gelegenheid te stellen, de bewegingen aan den bal mede te deelen, die de theorie aangeeft, en omgekeerd, weder verschijnselen in het leven te roepen, die door de natuurkundigen moeten worden uitgelegd. Deze theorie zelve behoort echter mede tot de meest ingewikkelde en zamengestelde in de leer der beweging; en op die wijze kan zij hier niet worden behandeld. Ik stel mij hier slechts voor, de uitkomsten der theorie zoo duidelijk en eenvoudig mogelijk af te leiden en hare oorzaken steeds te doen inzien. Daartoe zal het een en ander over de botsing tusschen twee ligchamen moeten voorafgaan.
Laat ons eerst stilstaan bij den schok van twee niet-veerkrachtige ligchamen, en ons dan tot volkomen en niet-volkomen veerkrachtige bepalen. Men kan zich hier het eene ligchaam, dat geschokt wordt, steeds in rust denken, zoo als dit bij het billard altijd het geval is; en daardoor worden de uitkomsten iets eenvoudiger.
Uit de ondervinding zoowel als door opzettelijke proefneming is het bekend, dat de snelheid van eenig voortbewogen ligchaam toeneemt met de kracht, die het voortdreef, en omgekeerd kleiner wordt, wanneer met dezelfde kracht een zwaarder ligchaam wordt voortgestuwd: en dit wel in dezelfde verhouding, zoodat de snelheid en het gewigt van het voortgedreven ligchaam, te zamen vermenigvuldigd, eene maat van de kracht aangeven, die men hoeveelheid van beweging pleegt te noemen. Zoo wordt de kracht, vereischt om b.v. aan 2 ௫ eene snelheid 15 te geven door 2 x 15 = 30, en die, welke 5 ௫? met eene snelheid 6 doet bewegen, door 5 x 6 = 30 voorgesteld; beide krachten zijn dus gelijk, dat is, men heeft dezelfde kracht noodig, om 2 ௫ met eene snelheid 15, als om 5 ௫ met eene snelheid 6 voort te stuwen.
Wanneer nu in ons geval een ligchaam A (van a ௫?) in rust is en door een ligchaam B (van b ௫) geschokt wordt, dat met zekere snelheid s aankomt: zoo zullen beide ligchamen, die hier vooreerst niet-veerkrachtig worden ondersteld, te zamen met eene zekere snelheid voortgaan. De kracht, die het ligchaam B bewoog, wordt naar het bovenstaande voorgesteld door bs, en diezelfde kracht moet nu de [ 67 ]twee ligchamen A en B, te zamen wegende a + b ௫ voortbewegen. Dit gezamenlijke gewigt (a + b) op de kracht bs doelende, komt er voor de gezamenlijke snelheid na den schok bs⁄a + b. Het ligchaam A, dat in rust was, heeft dus de snelheid bs⁄a + b gewonnen: het ligchaam B daarentegen, dat s snelheid bezat, en nu slechts bs⁄a + b snelheid overhoudt, heeft dus de snelheid as⁄a + b verloren. Gaat men na, hoe eigenlijk dit overdragen van snelheid, om het zoo eens te noemen, bij niet-veerkrachtige ligchamen geschiedt, dan ziet men in, dat bij den schok het bewegende ligchaam B door het ligchaam A iets moet worden ingedrukt: deze indrukking zal steeds afnemen, en juist dan ophouden, wanneer de snelheid van beide ligchamen gelijk geworden is. Omdat dan de indrukking heeft opgehouden, en de ligchamen niet-veerkrachtig zijn ondersteld, zoo blijven zij geheel in den toestand, waarin zij op dat oogenblik verkeerden, en beginnen hunne gezamenlijke beweging. Al die verschillende toestanden zullen elkander ongetwijfeld zeer snel opvolgen, maar er zal toch een zekere tijd toe noodig wezen: hoe groot of klein deze tijd ook zij, is echter onverschillig voor de uitkomst.
Maar zijn nu de ligchamen volkomen veerkrachtig, dat is, hebben zij de eigenschap om na verandering van gedaante den oorspronkelijken vorm weder aan te nemen, zoodra de storende invloed ophoudt, dan wordt het verschijnsel van anderen aard. Alles toch zal bij het indrukken van het bewegende ligchaam hetzelfde blijven, tot op het oogenblik, dat de snelheden gelijk zijn geworden: maar nu zijn de ligchamen met betrekking tot elkander niet in rust gekomen, zoo als straks de niet-veerkrachtige. Integendeel verkrijgen zij eerst nu de vrijheid om te trachten hunnen oorspronkelijken vorm wederom aan te nemen, en dit wel te meer, naarmate reeds de snelheid van het geschokte ligchaam toeneemt en die van het bewegende ligchaam afneemt. Er zal dus hier, bij volkomen veerkracht, na het gelijkworden der snelheden, juist hetzelfde, maar in omgekeerde orde, plaats hebben, wat er bij het begin van den schok gebeurde tot op het oogenblik, dat de ligchamen gelijke snelheid verkregen. Dientengevolge zal dus [ 68 ]ook het eerste ligchaam eene dubbele winst, het tweede een dubbel verlies in snelheid ondervinden; dat is: het eerste, dat in rust was, verkrijgt na den schok eene snelheid 2 bs⁄a + b, het tweede ligchaam, dat eene snelheid s had, heeft nu 2 as⁄a + b, verloren en dus slechts b - a⁄a + b s snelheid behouden.
Bij niet-volkomen veerkrachtige ligchamen zal het tweede gedeelte van het verschijnsel ook wel plaats vinden, maar in mindere sterkte dan het eerste; stel b.v. p maal (waar p in vele gevallen b.v. ½ kan zijn). Alsdan is de snelheid van het eerste ligchaam na den schok (1 + p) bs⁄a + b en het verlies in snelheid bij het tweede (1 + p) as⁄a + b dus beiden minder dan in het geval van volkomen veerkracht. Bij volstrekt gemis aan veerkracht wordt p gelijk nul, en zouden de eerst gevonden uitkomsten weder voor den dag komen.
Het bovenstaande is genoegzaam tot het regt begrip van hetgeen er bij het billard plaats grijpt. Vooreerst toch is in den regel de Queue of stok, waarmede men stoot, driemaal zoo zwaar als een bal; neemt men dus het gewigt van eenen bal voor de eenheid (= 1), zoo is de Queue 3. Nu is de Queue, al is zij van een goede kurken of lederen punt, de pommerance, voorzien, niet volkomen veerkrachtig, en proeven dienaangaande hebben aangetoond, dat hier p = 11⁄15 is. Stoot dus de Queue tegen eenen bal, die stil ligt, zoo verkrijgt deze eene snelheid (1 + 11⁄15) 3⁄3 + 1 = 13⁄10 van de snelheid der Queue. Men maakt uit de formule gereedelijk op, dat eene zwaardere Queue (waarbij b grooter is) ook eene grootere snelheid zal mededeelen, terwijl die bij eene ligtere Queue kleiner wordt: er zijn echter andere omstandigheden, later te beschouwen, die eene Queue van de zwaarte van drie ballen voor het gebruik meest geschikt maken.
Stoot echter de eene bal tegen den anderen, en wel in de rigting, die hunne middelpunten vereenigt,—dus bij eenen zoogenaamden centralen stoot,—zoo zijn hier de gewigten der ballen gelijk; en daar zelfs bij goede ivoren ballen de veerkracht niet volkomen kan [ 69 ]ondersteld worden (p is = 0,94), zoo verkrijgt de bal, die gestooten wordt, en dien wij de speelbal noemen, 0,97 van de snelheid van den stootenden bal, den handbal; terwijl deze nog 0,03 van zijne snelheid behoudt. Waren zij volkomen veerkrachtig, dan zoude de speelbal alle snelheid overnemen en de handbal in volstrekte rust geraken.
Wanneer men den handbal loodregt tegen eenen der zijwanden van het billard, den band, speelt, dan bevindt men, dat deze niet volkomen veerkrachtig is: uit proefneming blijkt nu, dat hier p = 11⁄20 is. Maar eene andere vraag is hier, hoeveel is het gewigt van dien band? Deze is een ligchaam, dat vast staat, en dus geene voortgaande beweging kan verkrijgen door den schok van den bal. Bijna hetzelfde zoude het geval zijn, wanneer een geschokte bal oneindig zwaar was, dat is zóó zwaar, dat het gewigt van den stootenden bal daarbij niet in aanmerking zoude komen: dat er dus tusschen het gewigt van dien bal vóór den schok en het gewigt bij den schok, als de stootende bal daarbij te rekenen is, betrekkelijk weinig of geen verschil bestaan, of dat a⁄a + b nagenoeg gelijk één zoude zijn. Wanneer dus, zoo als hier, de band volstrekt geene snelheid verkrijgt, dus b⁄a + b juist nul is, alsdan is ook a⁄a + b = 1—b⁄a + b juist gelijk aan de eenheid. De stootende bal verliest dus juist (1 + p) maal zijne oorspronkelijke snelheid. Waren de band en de bal beide volkomen veerkrachtig, zoo verloor de bal tweemaal zijne snelheid (voor p=1), dat is, hij kreeg zijne oorspronkelijke snelheid terug, maar in tegengestelde rigting; nu echter bij het billard de band niet volkomen veerkrachtig en p hier slechts = 11⁄20 is, zoo verkrijgt de bal slechts 11⁄20 van zijne oorspronkelijke snelheid in tegengestelde rigting, dat is, hij verliest 111⁄20 van zijne oorspronkelijke snelheid.
Uit het overwogene is nu gemakkelijk op te maken, wat er gebeuren moet, wanneer de rigting van den stoot tusschen twee ballen niet met de verbindingslijn der middelpunten overeenkomt, of de rigting van den stoot op den band niet loodregt daarop staat. Hiertoe behoeft men het bekende beginsel uit de leer van evenwigt, het parallelogram der krachten; waaruit men leert, dat eene kracht, werkende volgens [ 70 ]de diagonaal van een parallelogram, volkomen dezelfde uitwerking heeft als twee krachten te zamen, die elke volgens eene der twee zijden van het parallelogram werken, welke hetzelfde hoekpunt met de diagonaal gemeen hebbe; wanneer slechts alle drie krachten in denzelfden zin werken en de lengte der genoemde lijnen zelve hare maat voorstelt. Men zegt dan, dat de kracht volgens de diagonaal ontbonden is in de beide krachten volgens de zijden: en omgekeerd, dat beide laatste krachten zijn te zamen gesteld tot de kracht volgens de diagonaal, hare resultante: en dit alles zoowel in rigting als in grootte.
Raakt dus de handbal den speelbal in eene rigting AH, (Fig. 1.)
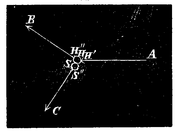
Fig. 1.
Fig. 2.
schuins staande op de verbindingslijn der middelpunten HS (bij eenen zoogenaamden schuinschen stoot), zoo kan men voor de snelheid van den handbal of liever voor de kracht HA (Fig. 2), die daarvan als oorzaak wordt aangenomen, twee andere krachten HB en HC, in de plaats stellen, waarvan de eene HC gerigt is volgens die verbindingslijn, de andere HB volgens eene lijn, die de beide ballen in hun raakpunt aanraakt. De laatste kracht HB zal slechts te weeg brengen, dat de handbal zich in die rigting na den schok voortbeweegt, en zal op den schok geenen invloed uitoefenen. Anders is het met de eerste kracht HC, die eigenlijk alleen den schok te weeg brengt: op deze blijft het vroeger gezegde volkomen toepasselijk. Nemen wij voortaan, daar wij ons toch met benaderde uitkomsten hier moeten tevreden stellen, de ballen als volkomen veerkrachtig aan, dan verliest de handbal alle snelheid volgens de rigting der lijn, die de middelpunten vereenigt, en deze snelheid gaat geheel op den speelbal over. Na den schok dus verkrijgen de speelbal en de handbal bewegingen, waarvan snelheid en rigting (Fig. 1) worden voorgesteld door de ontbondenen van de [ 71 ]kracht AH' van den handbal in de rigting van de verbindingslijn der middelpunten (S"C), en in eene rigting loodregt daarop (H"B); want de laatste lijn, de gemeenschappelijke raaklijn aan beide cirkels, staat loodregt op de eerste.
Wanneer de handbal eenen band volgens eene schuinsche rigting raakt,
Fig. 3.
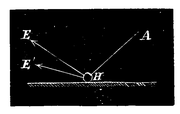
Fig. 4.
is het verschijnsel weder eenigzins anders. Men ontbinde (Fig. 4) wederom de snelheid van den bal AH in twee rigtingen, de eene AB in de rigting van den band, de andere AC loodregt op die rigting: de eerste doet niets tot den schok, die alleen ten gevolge van de tweede ontstaat. Was nu de band volkomen veerkrachtig, dan zoude die loodregte snelheid na den schok slechts van rigting veranderen, en wanneer men nu deze nieuwe snelheid HB met de onveranderlijk gebleven snelheid HD in de rigting van den band te zamen stelt tot eene enkele, verkrijgt men eene nieuwe kracht HE, juist gelijk aan de oude AH, en die met den band eenen even grooten hoek maakt, maar in tegengestelden zin. En dit is de zoo bekende natuurwet, die bij de theorie van geluid, warmte en licht steeds hare toepassing vindt: de hoek van inval (∠ AHC) is gelijk aan den hoek van terugkaatsing (∠ EHD). In ons geval evenwel, waar de band niet volkomen veerkrachtig en p dus niet gelijk 1, maar = 11⁄20 is, wordt de snelheid, loodregt op den band na den stoot, HB' slechts 11⁄20 van de oorspronkelijke AC en in tegengestelde rigting; deze weder met de onveranderde snelheid HD langs den band te zamen stellende, wordt de nieuwe snelheid na den stoot HE' kleiner, en maakt zij eenen kleineren hoek met den band, dan volgens de gemelde wet met HE zoude plaats grijpen.
En hiermede zouden alle voorkomende gevallen beschouwd en [ 72 ]de theorie van het billard zijn afgehandeld, ware het niet, dat wij tot nog toe eene zeer belangrijke storing hadden verwaarloosd, die dit spel juist zoo belangrijk, maar ook zoo leerzaam maakt: zooveel mogelijk zal ook deze invloed nader worden opgehelderd. Al het voorgaande geldt onvoorwaardelijk, wanneer de beweging geheel vrij ware: maar dat is zij niet. Eensdeels de tegenstand der lucht, ten andere die van het vlak, waarover de ballen zich bewegen, oefenen invloed op die beweging uit. De snelheden echter, die wij door het stooten met de Queue mededeelen, zijn veel te gering, dat de invloed van den tegenstand der lucht merkbaar zoude worden: gerustelijk mag men dien derhalve verwaarloozen. Anders is het met den tegenstand, door de beweging op het vlak geboren. Was dit vlak volkomen plat, en was de bal volkomen rond, dan zoude die tegenstand verdwijnen: maar nu is elk vlak met meer of minder groote hobbeligheden voorzien, naarmate wij het ruw of glad noemen: bij het laken op het billard is dit ontegenzeggelijk het geval: maar evenzeer bij den ivoren bal, hoe zuiver ook gedraaid, hoe glad ook gepolijst. Wanneer men bijv. een microscoop gebruikte, dat genoegzaam vergrootte, zoude men bij het punt, waar de bal op de tafel rust, de beide oppervlakken ongeveer in eenen toestand vinden, als hier is aangegeven in Fig. 5.
Fig. 5. Het vlak van de tafel heeft diepten, waarin de verhevenheden van den bal, onvolkomen echter, komen te rusten. Beweegt zich nu de bal vooruit op de tafel, zoo is er eene zekere kracht noodig, om die verhevenheden van den bal als het ware uit de diepten op te tillen en over de hoogten heen te trekken: tracht de bal te rollen, dan heeft iets dergelijks plaats. Men kan zich van deze tegenstanden en hunne betrekkelijke grootte een denkbeeld maken door op eene niet al te gladde oppervlakte, dat volmaakt waterpas staat, twee ligchamen te leggen, eenen bal b.v. en een plankje, waarvan de eerste slechts een punt, het tweede een vlak met de genoemde oppervlakte gemeen heeft. Tilt men deze oppervlakte nu voorzigtig en langzaam aan de eene zijde in de hoogte, dan zal, bij eene zekere helling, de bal, [ 73 ]en eerst bij meerdere optilling ook het plankje aan het glijden gaan. De hoogte, waartoe men de oppervlakte moet optillen, zal minder zijn naarmate deze gladder is. De oorzaak van deze verschijnselen is nu niets anders dan de straks verklaarde tegenstand, en deze heet wrijving.
Passen wij dit op ons billard toe, dan ziet men, dat b.v. bij eene tafel van zuiver geslepen glas, die tegenstand niet zoo groot zoude wezen, als nu die tafels met fijn laken zijn bekleed: daardoor wordt de beweging der ballen veel sterker belemmerd. Dit is echter geene fout: integendeel, eerst op die wijze kan men de dikwerf verrassende bewegingen verkrijgen, die een geoefend speler aan zijnen bal weet mede te deelen, en waarvan wij nu in de volgende behandeling de verklaring zullen vinden.
Wrijving is, zoo als is opgemerkt, in het algemeen de tegenstand, die bij de beweging van eenig ligchaam over een ander wordt voortgebragt. Is de beweging niet alleen eene voortgaande, maar ook eene draaijende, zoo is de wrijving van tweederlei aard: vooreerst die, welke door de schuring van het voortgaande, voortschuivende ligchaam ontstaat, de slepende wrijving: ten andere die, welke door het rollen, het ronddraaijen ontstaat, de rollende wrijving. Bij het billard komt deze laatste niet in aanmerking, wel de eerste; en voorloopig kan reeds worden opgemerkt, dat zij niet gering is: dit volgt toch reeds daaruit, dat een bal met weinig snelheid deze al zeer spoedig verliest, alleen ten gevolge natuurlijk van die wrijving. Wordt nu een bal voortbewogen, dan zal de uitwerking van de wrijving wezen, om de vooruitgaande beweging van het onderste punt, dat wij het steunpunt van den bal zullen noemen, te verhinderen. Bestond de bal enkel uit losse stofdeelen, dan zouden de hooger gelegen stofdeelen blijven voortgaan, en het stofdeel in het steunpunt telkens blijven liggen: dit is echter niet zóó, de stof van den bal wordt door de cohaesie te zamen gehouden; de hooger gelegen deelen trachten desniettemin vooruittegaan, terwijl het steunpunt oogenblikkelijk wordt opgehouden; en ziedaar, de bal begint zich te wentelen. De invloed van de wrijving is dus, eene ronddraaijende beweging aan den bal te geven. Maar alle punten van den bal bewegen zich daarbij niet even snel. Alleen het steunpunt is tijdelijk in rust, en van daar langs de middellijn opklim[ 74 ]mende tot aan het tegenovergestelde punt van den bal, het bovenpunt, heeft ieder punt eene grootere beweging: dit ontstaat niet door den oorspronkelijken stoot, dien wij vooralsnog eenen centralen onderstellen,—daardoor zouden alle punten van die middellijn zich even snel moeten bewegen,—het is een gevolg van de wrijving. Stelt men zich ieder punt van den bal op zich zelf voor, dan zijn er eenige, die zich nu niet zoo snel kunnen bewegen, als zij alleen ten gevolge van den stoot zouden doen, ja er zijn er, die nu eene juist tegengestelde beweging verkrijgen;—andere punten zijn er daarentegen, waarvan de snelheid der beweging grooter is geworden. Men kan het zich dus voorstellen, alsof de eersten als het ware worden opgehouden in hunne beweging, de laatsten daarentegen nog worden voortgestuwd. Het is nu wel te vermoeden, dat er toch één of meer punten zullen te vinden zijn, die zich bij deze zamengestelde beweging geheel vrijelijk zullen bewegen, dat is, die noch opgehouden noch voortgestuwd worden, maar hunne eigene beweging behouden: en de theorie bevestigt dit, als zij ons leert, hoe het eenige punt, waarvan de beweging niet gestoord wordt,—en dat slingerpunt, middelpunt van percussie wordt genoemd naar andere zamenhangende eigenschappen, die dit punt bezit,—hoe dit punt voor elken bijzonderen vorm van het draaijende ligchaam eene bepaalde plaats verkrijgt. Bij eenen gelijkslachtigen of homogenen bal, dat is, zulk eenen, waarvan de stof overal dezelfde en even digt is, ligt dit punt op de middellijn, die door het steunpunt gaat, en wel op eenen afstand boven het middelpunt, gelijk aan twee vijfde deelen van den straal (het punt P, Fig. 6), en dit 
Fig. 6. punt zal dus juist, als het ware, de gemiddelde snelheid bezitten, die de wrijving zoowel als de toegebragte stoot moeten teweegbrengen.
Keeren wij, na deze noodzakelijke uitweiding, tot het billard terug. Is de bal zoodanig voortgestooten, dat daardoor op zich zelf geene draaijing zoude ontstaan,—en dat is het geval bij eenen centralen stoot, dat is zulk eenen, waarbij de rigting van den schok door het mid[ 75 ]delpunt gaat,—dan heeft de wrijving draaijing ten gevolge, en verandert daardoor de snelheid van het slingerpunt, totdat er geene enkel voortstuwende kracht meer is overgebleven, maar deze geheel door de wrijving is overwonnen; maar dan is er ook tevens geene wrijving meer, en de bal rolt, zoo als men pleegt te zeggen, hij is in zijnen eindtoestand overgegaan. De uitwerking der wrijving kan derhalve slechts invloed hebben, voor dat de bal in dien eindtoestand overgaat; en dit geldt niet alleen bij dezen bepaalden stoot, maar bij alle stooten in het algemeen. Men kan toch door middel van de Queue, die met eene pommerance voorzien is, den stoot nog anders aanbrengen dan juist door het middelpunt, en daarboven of daaronder, of ook nog daarnaast stooten. Die laatste stooten zullen wij nu voor het oogenblik achterwege laten, en eerst de uitwerking dier stooten beschouwen, waarbij de rigting van den stoot in een vlak ligt, dat door het middelpunt van den bal gaande loodregt staat op het vlak van de tafel, zoo als de oppervlakte pleegt genoemd te worden, waarover de bal zich moet bewegen.
Vooreerst kan de stoot zóó gerigt zijn, dat hij door het slingerpunt gaat; alsdan zal er, naar het gezegde, volstrekt geene wrijving plaats hebben, maar de bal dadelijk zijnen eindtoestand bereiken, en blijven voortrollen. De stoot zoude ook boven het slingerpunt aangebragt kunnen worden, en dan zoude de werking van de wrijving worden versterkt; maar praktisch is dit van weinig nut, dewijl het zeer moeijelijk is, den bal aldaar zuiver te raken, zonder, zoo als men zegt, fausse queue te maken, dat is, zóó te stooten, dat de Queue zijdelings afglijdt. Daarbij wordt dan, behalve de mededeeling der beweging door den stoot zelven, nog eene wrijving of schuring van de Queue op den bal teweeggebragt, die den loop van den bal ten eenenmale verstoort, zoodat er alsdan eene geheel andere beweging aan den bal wordt medegedeeld, dan bedoeld werd: deze heeft tevens het nadeel van volstrekt niet bepaald of berekend te kunnen worden, en komt dus verder niet in aanmerking.—Maar eerder kan de stoot onder het slingerpunt plaats vinden: alsdan ontstaat er, behalve de voortgaande beweging, nog eene draaijende, en nu wel in eene rigting, tegengesteld [ 76 ]aan die, welke ten gevolge der wrijving wordt geboren. Naarmate men lager raakt, wordt deze draaijing sterker: van het lager stooten zoowel als van de kracht van den stoot hangt het nu af, of die draaijing sterker of zwakker zal zijn dan die, waarvan de wrijving de oorzaak is. Is zij zwakker, dan dient het overschot, om den bal door de wrijving te laten draaijen: maar is zij integendeel sterker, dan zal het verschil moeten teweegbrengen, dat de bal ronddraait juist in tegengestelden zin van zijne gewone omwenteling. Zulk een stoot, waarbij echter het lager, zwakker stooten gewoonlijk de voorkeur verdient boven het minder laag maar sterker stooten, heet pommeranceren. Nu is het duidelijk, dat de wrijving gedurig blijft werken zoolang er beweging is, terwijl deze tegengestelde omwenteling het gevolg is van eenen slechts oogenblikkelijken stoot: de wrijving zal deze werking dus langzamerhand overwinnen, tot dat hare eigene werking alleen overblijft. Wanneer men dus den bal in dien toestand van draaijing brengt, waarbij deze tegengesteld is aan de gewone rigting, dan volgen de verschijnselen zich aldus op: Eerst heeft de bal deze rotatie in tegengestelden zin, die wij dus negatieve rotatie zullen noemen, door de wrijving wordt zij allengs verminderd, totdat zij nul wordt, en de bal alleen, zonder om te wentelen, over de tafel heenschuift: dit duurt slechts een enkel oogenblik; vervolgens doet de wrijving den bal in den gewonen zin ronddraaijen (dat wij dan positieve rotatie noemen), tot dat die wrijving al minder en minder werkt, en eindelijk de bal in zijnen eindtoestand overgaat en begint te rollen. De bal verkeert dus achtereenvolgens in vier geheel verschillende toestanden, die elkander evenwel vrij snel opvolgen, terwijl de laatste, de eindtoestand, in den regel verreweg het langste duurt. En verschillend zullen dus ook de verschijnselen moeten zijn, naarmate de handbal of tegen den speelbal of tegen den band schokt, terwijl hij zich oogenblikkelijk in eenen dier toestanden bevindt.
Is dan vooreerst de stoot van den handbal op den speelbal in de rigting die hunne middelpunten vereenigt, dan zal de speelbal altijd worden vooruitgestooten in diezelfde rigting, met eene snelheid, die slechts afhangt van de snelheid van den handbal op het oogenblik van den schok, geenszins van den toestand, waarin deze dan verkeert. Die [ 77 ]handbal daarentegen zal na den schok eene beweging aannemen, die van zijnen toestand op dat oogenblik afhangt: hij zal na de botsing terugloopen, blijven liggen, of met den speelbal mede vooruitloopen, naarmate hij vóór de botsing eene negatieve draaijing bezat, of alleen gleed, zonder omwenteling, of in eenen positieven zin draaide. Het laatste is uit zich zelf duidelijk. Als de bal slechts glijdt op het oogenblik van den schok, zonder om te wentelen, is hij in het geval, dat wij reeds vroeger beschouwden, toen de wrijving nog niet in aanmerking genomen werd: de bal moet dus hier, even als daar, na de botsing stil blijven liggen, althans bij volkomen veerkrachtige ballen. Heeft eindelijk de bal op het oogenblik van den schok eene negatieve rotatie, zoo zal door de botsing de werking van de wrijving worden opgeheven en slechts die negatieve ronddraaijing overblijven, die aan den stoot van de Queue verschuldigd is, voor zooverre zij althans nog bestaat: en nu moet ten gevolge dier negatieve draaijing de bal natuurlijk terugrollen. Hieruit volgt tevens, dat de botsing de voortgaande snelheid aan den handbal ontneemt, en deze dus slechts de bijkomende draaijing overhoudt, zoodat het op de rigting dier omwenteling slechts aankomt, dat is, dat de bal na de botsing in zijnen eindtoestand gekomen is, bij welken toestand die botsing ook moge plaats gehad hebben.
Beschouwt men nu vervolgens den schok van den handbal tegen den band, dan ziet men naar het voorgaande gemakkelijk, dat de bal zal blijven liggen, wanneer hij tijdens den schok juist in eenen toestand van glijding verkeert. Is dit niet het geval, dan moet de bal terugkeeren, hetzij hij positief of negatief ronddraaide, en daarbij zal er slechts onderscheid bestaan in de snelheid, die de bal na den schok bezit, terwijl de toestand, waarin hij verkeert, steeds weder zijn eindtoestand is.
Op dezelfde wijze verklaren zich de verschijnselen zeer gemakkelijk, die er bij eenen schuinschen stoot zich voordoen; dat is, wanneer bij de botsing tusschen hand- en speelbal, die wij wederom het eerst zullen nagaan, de rigting van den stoot niet overeenkomt met de ver[ 78 ]bindingslijn der middelpunten. Men heeft daarbij slechts op te merken, dat de schok invloed uitoefent op de voortgaande beweging, maar daarentegen de draaijing zelve in geenen deele verstoort, zoodat die draaijende beweging op zich zelve voor en na den schok dezelfde is gebleven. Maar hier, bij den schuinschen stoot, blijft er, zoo als wij straks gezien hebben, voor dat de wrijving in aanmerking kwam, nog voortgaande beweging over, en wel in de rigting van de gemeenschappelijke raaklijn aan beide ballen. Deze beweging, in zoo verre zij het gevolg is van den oorspronkelijken stoot der Queue, is dus gelijkmatig, daar deze stoot slechts oogenblikkelijk werkte: niet alzoo de beweging, die ten gevolge der wrijving ontstaat; deze is eene kracht, die gedurig werkt: en de beweging is dus niet meer gelijkmatig, maar versneld. Zoodra nu beide deze krachten niet meer in dezelfde rigting werken, en dit is hier het geval geworden, houdt de regtlijnige beweging op, en de bal beweegt zich langs eene kromme lijn, en wel onder de omstandigheden, die hier in aanmerking komen, in eene parabool. Die omstandigheden komen in vele opzigten overeen met die, welke bij de beweging van een in de schuinte opgeworpen ligchaam, van eenen bom b.v., te onderscheiden zijn. Deze zoude tengevolge der voortwerpende kracht van de mortier (of van de lading daarvan, als men liever wil), wel eene regte lijn beschrijven, maar door de gedurige werking der zwaartekracht wordt de bom telkens van hare rigting afgetrokken: zij verkrijgt daardoor eene kromlijnige, en wel eene parabolische beweging, zoo als uit de leer der beweging bekend is. Hier, in ons geval, treedt de wrijving in de plaats van de zwaartekracht en de Queue vervangt de mortier. De uitkomsten zijn dus dezelfde en de beweging van den bal na den schok is kromlijnig geworden; en wij hebben thans eene groote schrede gedaan tot de verklaring der zoo bijzondere uitwerking van eenen bal op het billard. Passen wij nu het gezegde toe op den schuinschen stoot tegen den speelbal, en onderscheiden wij daarbij de bijzondere gevallen, dat de handbal in eenen der vroeger beschouwde toestanden verkeert.
Was de handbal op het oogenblik van den schok in den toestand van enkele wrijving zonder draaijing, dan blijft de uitkomst dezelfde, als of er geene wrijving ware, en die wij vroeger hebben nagegaan; [ 79 ]alsdan toch werkt de wrijving niet storend, en er ontstaat door haar geene rotatie, die den bal van de regte lijn zoude doen afwijken. De handbal beweegt zich Fig. 7[1] volgens de lijn H 1, in juist dezelfde 
Fig. 7. rigting als Fig. 1 het geval was, toen de wrijving nog niet in aanmerking werd genomen. Bij de overige toestanden heeft de wrijving als het ware niet uitgewerkt, en veroorzaakt dus, na den schok, eene kromlijnige beweging. Is de draaijing positief, die door den stoot is medegedeeld, dat is, wordt de uitwerking der wrijving nog versterkt, zoo zal de bal trachten zich verder te bewegen, dan zijne eigenlijke rigting, de raaklijn aan beide ballen, naar zijne oorspronkelijke rigting toe: de bal beschrijft dan eene parabool H 2, waarvan de bolle zijde gekeerd is naar den kant, waarvan de bal zich voor den stoot bewoog. Bevindt de bal zich op het oogenblik van den schok in eenen toestand van negatieve draaijing, zoo tracht de bal zich terug te bewegen naar de rigting, vanwaar hij gekomen is: de parabool H 3 is dan omgekeerd gelegen, met hare holle zijde naar den kant, vanwaar de handbal gekomen is. Was de bal eindelijk bij den schok reeds in zijnen eindtoestand, dan is de draaijing weder in denzelfden zin, als hiervoor bij glijding en positieve draaijing, maar de parabool H 4 zal veel minder sterk gekromd zijn: de reden daarvan is ligtelijk te bevroeden. Zoolang toch de bal niet in zijnen eindtoestand gekomen is, wordt hij door [ 80 ]de wrijving als het ware opgehouden; deze bestaat hier niet meer, er is slechts de draaijing overgebleven en dus ontstaat ook hier de parabool, met hare bolle zijde naar den kant gekeerd, vanwaar de schok plaats greep; maar deze moet hier minder van de regtlijnige rigting afwijken, dan straks het geval was bij H 2, want het meerdere in de positieve rondwenteling, dat door het hoog raken van den bal geboren werd, ontbreekt hier.
Fig. 8.
Verkeert de bal bij den schok slechts in eenen toestand van glijding, dan heeft de wrijving geenen storenden invloed op de beweging van den schok, en heeft men wederom dezelfde uitkomst als in Fig 3, waar de wrijving en hare gevolgen nog niet in aanmerking kwamen; de beweging is regtlijnig H 1, en maakt met den band eenen hoek, niet zoo groot als die, waaronder de bal op den band invalt, en dat wel, zoo als wij vroeger zagen, omdat de band niet volkomen veerkrachtig is. Wanneer wij nu den invloed, die de andere toestanden van den bal bij den schok uitoefenen, vergelijken bij hetgeen hier gebeurt, zoo zien wij, dat daarbij wederom eene kromlijnige beweging moet ontstaan, omdat de wrijving nog niet heeft opgehouden te werken. Was de draaijing van den bal in eene positieve rigting, zoo zal zich deze, na den schok tegen den band, meer naar dien band trachten te begeven: hij beweegt zich dus weder in eene parabool H 2, die met de holle zijde naar den band is gekeerd. Was daarentegen de omwenteling van den bal negatief op het oogenblik van den schok tegen den band, zoo tracht de bal na dien schok zich nog meer van den band te verwijderen, dan bij het geval, [ 81 ]toen hij in eenen toestand van enkele glijding tegen den band stootte; de beweging geschiedt dien ten gevolge in eene parabool H 3, waarvan nu de bolle zijde naar den band is gekeerd. Bezat eindelijk de bal geene wrijving, maar bevond hij zich bij den schok tegen den band reeds in zijnen eindtoestand, zoo werkt na dien schok de enkele draaijing nog in dien zin, dat zij den bal tracht vooruit te bewegen, meer dan zijne vroegere regtlijnige beweging zoude toelaten. Er ontstaat dus alsdan ook eene parabool H 4, van dezelfde ligging als H 2, maar waarvan de kromming minder zal moeten zijn, omdat de draaijing, die hier slechts door de wrijving ontstaan is, minder sterk is dan daar, waar zij tevens door den hoogen stoot werd voortgebragt, en dus ook hier slechts eene mindere afwijking van de regte lijn ten gevolge kan hebben dan daar.
Bij de schuinsche stooten, hier beschouwd, moet nog worden opgemerkt, dat na den schok de bal in het algemeen nog niet in zijnen eindtoestand gekomen is, zoo als onder dezelfde omstandigheden het geval bleek te zijn bij regte stooten: de reden daarvan is duidelijk, daar bij den schuinschen stoot nog regtlijnige beweging overblijft, die bij den regten stoot geheel werd weggenomen.
Het hier gezegde moge genoeg zijn om de verschillende uitwerkingen te doen kennen van de stooten, die den bal raken in een vlak, door het middelpunt loodregt op de tafel staande. Het kan hier natuurlijk de bedoeling niet wezen, om de verschillende parabolen te leeren construeren, evenmin om te berekenen, wanneer de verschillende uitwerkingen in een of ander opzigt het sterkst of het kleinst, dat is, in meer wetenschappelijke termen, een maximum of een minimum zullen worden. Daartoe zoude men tot een stel formulen geraken, dat hier niet op zijne plaats zoude zijn. Wij willen liever eerst de volgende figuren eens bezien, die den loop van den handbal voorstellen, wanneer de schok in eenen verschillenden toestand plaats heeft, om daarna nog de eene of andere algemeene opmerking te doen volgen.
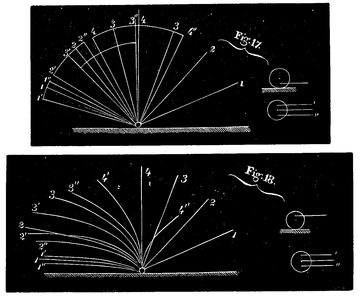
[ 82 ]
In Fig. 9 tot 13 is de beweging van den handbal en den speelbal voorgesteld, naarmate de stoot regt is (deze is met 0 aangeduid), of naarmate de verbindingslijn der middelpunten, waarmede de rigting van den speelbal na den schok moet zamenvallen, 11⁄4, 2⁄4 of 3⁄4 van eenen regten hoek met de rigting van den regten stoot maakt; dat is, naarmate die verbindingslijn gerigt is volgens de regte lijnen, die met 1, 2, 3 gemerkt, aan de linkerzijde der figuren zijn getrokken: de overeenkomstige kromme lijnen, die dan door den handbal worden beschreven, zijn met dezelfde cijfers 1, 2, 3 gemerkt, en zijn natuurlijk aan de regterzijde der figuren te vinden. De handbal is laag gestooten, zoo als in de bijgevoegde figuur is aangeduid: maar de verschillende bewegingen hangen af van den toestand, waarin de handbal op het oogenblik van den schok verkeert. In Fig. 9 is de schok geschied bijna dadelijk na den stoot, in Fig. 10 iets later; bij beiden echter verkeert de bal in eenen toestand van negatieve draaijing: van daar, [ 83 ]dat de bolle zijde van de parabolen naar de lijn 0 is gekeerd. In Fig. 11 was de handbal in eenen toestand van enkele glijding: na den schok beweegt hij zich dus volgens eene regte lijn. In Fig. 12 bezit de handbal eene positieve draaijing, en in Fig. 13 heeft hij zijnen eindtoestand bereikt: vandaar is in de beide laatste gevallen de holle zijde der parabolen naar de lijn 0 gerigt; slechts zijn de parabolen in Fig. 12 minder gekromd dan die in Fig. 13.
Fig. 14.
Fig. 15.
In Fig. 14 en 15 is de loop der ballen na den schok voorgesteld, wanneer de handbal niet meer laag, maar daarentegen zeer hoog gestooten is, zoo als in de bijgevoegde figuur is aangegeven. Bij Fig. 14 is de bal nog niet in den eindtoestand gekomen en behoudt de stoot zelf invloed; bij Fig. 15 is weder de eindtoestand daar, en zijn derhalve de parabolen in dit laatste geval minder gekromd, dan straks. De kromming der parabolen is weder naar den kant gerigt, die vroeger door de beschouwing werd aangewezen.
Vervolgens hebben wij hier uit de theorie zoowel als uit de proefnemingen een paar feiten mede te deelen, die bij de practische toepassing van het bovenstaande kunnen te pas komen.
Wanneer men de wrijving in aanmerking neemt, die uit proefnemingen op het billard blijkt gelijk te staan met eene kracht, die eene snelheid van 2½ meter in eene seconde zoude mededeelen, dient men ook de kracht te kennen, die den bal voortbeweegt, en die vroeger slechts als eenheid behoefde aangemerkt te worden, daar er steeds alleen evenredige deelen daarvan in aanmerking kwamen. Die kracht nu is uit den aard der zake zeer verschillend, maar blijft toch binnen zekere [ 84 ]grenzen beperkt; daar bij eene al te heftige beweging der Queue het ligt voorkomen kan, dat de Queue en de bal elkander na het oogenblik van de botsing nog blijven aanraken, dat de bal nagestooten wordt; en dit zoude den loop van den bal weder vertragen, en daarbij eenen storenden invloed op dien loop uitoefenen, even als wij dit bij eene fausse-queue zagen gebeuren. De sterkste stoot wordt nu gewoonlijk berekend op 7 meters per seconde, de gewone op 5 meters, de zwakste op 1 meter in de seconde.—Bij den eersten is nu, bij eenen stoot tegen den band, p = 0,5: bij den laatsten 0,6: bij de gewone stooten 0,55, zoo als reeds boven is opgegeven.—Bij eenen stoot van 7 meters door het middelpunt loopt de bal 5 meters af, eer hij zijnen eindtoestand bereikt: bij eenen stoot van 5 meters daarentegen, is dit reeds na 2½ meter het geval.—De hoogste en laagste punten, waar men den bal kan raken, zonder eene fausse-queue te maken, liggen op 6⁄10 deelen van den straal ter wederzijde van het middelpunt; men zal echter in den regel tot dien grens niet kunnen geraken. Voor eene ligtere Queue, die slechts even veel weegt als twee en een halve (in plaats van drie) ballen, heeft men voor dezen grens 7⁄10 deelen van den straal, dus iets meer dan gewoonlijk.
Wil men, bij eenen stoot van gegevene kracht, den bal zoo lang mogelijk de eigenschap doen behouden van bij eenen schok eene teruggaande beweging aantenemen, zoo moet men stooten op ¼ van den straal beneden het middelpunt: dan behoudt de bal b.v. voor eenen gewonen stoot van 5 meters deze eigenschap gedurende 1¾ meter, voor eenen stoot van 7 meters echter gedurende 31⁄3 meter. Indien men daarentegen, bij eenen stoot van gegevene kracht, den eindtoestand zoo laat mogelijk wil doen ontstaan, dan stoote men op 1⁄10 van den straal beneden het middelpunt: voor eenen stoot van 7 of 5 meters komt de bal alsdan na 53⁄4 of 23⁄4 meters respectievelijk eerst in zijnen eindtoestand.
Bij al deze stooten, en wel te meer naarmate de stoot lager is, komt in de praktijk de oefening van den speler te pas. Bij het gezegde toch is natuurlijk ondersteld, dat er na den stoot geene aanraking of wrijving meer tusschen Queue en handbal plaats hebbe, waardoor de draaijende beweging en daarmede de kracht [ 85 ]van den bal zouden gewijzigd worden. Bij lage stooten vooral geschiedt nu deze aanraking zeer ligt, indien de speler zich daarvoor niet wacht; een noodzakelijk vereischte tot het voorkomen hiervan volgt reeds uit de theorie, namelijk dat de Queue na den schok kunne terug springen, ten minste niet zoo snel vooruitgaan als de bal; men kan dit bevorderen door de Queue los in de hand te houden en liever dadelijk na den stoot iets terug te trekken; men kan dit evenzeer tegenwerken door de Queue vast in de hand te houden en den arm aan het ligchaam te sluiten, zoodat dan het gewigt van den arm bij het gewigt van de Queue komt, hare hoeveelheid van beweging vermeerdert, en dus de Queue na den schok eerder vooruit bewogen wordt tegen den bal aan; waardoor dan de negatieve draaijing belemmerd wordt.
Als men daarentegen den bal op 1⁄5 van den straal boven het middelpunt raakt, zoo verkrijgt deze, bij eene gegevene kracht van stooten, de eigenschap van hetzij voor, hetzij gedurende den eindtoestand, de grootst mogelijke snelheid te bezitten: deze is dan voor eenen stoot van 7 meters 59⁄20 meter, voor eenen gewonen stoot van 5 meters, slechts 22⁄5 meter. In het algemeen behoudt de bal, wanneer hij in zijnen eindtoestand is aangekomen, 5⁄7 van de snelheid, die hem oorspronkelijk is medegedeeld; en daar deze snelheid wederom 13⁄10 van die der Queue is, heeft de bal in zijnen eindtoestand ongeveer de snelheid der Queue; wel te verstaan, indien, zoo als hier overal ondersteld wordt, de Queue driemaal zoo veel weegt als de bal.
Keeren wij terug tot onze vroegere beschouwing. Tot nog toe gingen wij de beweging na van eenen bal, die door den horizontalen stoot der Queue eene ronddraaijende beweging verkreeg in denzelfden, of in juist tegengestelden zin als de rondwenteling, die een gevolg is van de wrijving; dat is, de bal draaide om eene horizontale as, loodregt op de rigting, waarin de bal zich voortbewoog. Maar men kan evenzeer, ook bij eenen horizontalen stoot der Queue, den bal in eenig punt raken, dat niet valt in het loodregte vlak, dat het middelpunt en de rigting van den stoot bevat: dat is,—wanneer Fig. 16 de doorsnede van den bal voorstelt, loodregt genomen op de rigting van den stoot, — [ 86 ]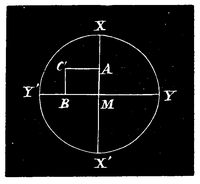
de stoot behoeft niet door een punt van de loodregte middellijn XX' te gaan, men kan den bal ook in eenig punt C raken. De ondervinding leert, dat alsdan bij den schok de bal, als het ware voor een enkel oogenblik slechts, één ligchaam met de Queue uitmaakt, en dien ten gevolge eene voortgaande beweging verkrijgt juist in dezelfde rigting als die der Queue; althans wanneer er een gewone stoot plaats heeft, want bij eene fausse-queue deelt de Queue door het afglijden langs den bal aan dat ligchaam ook eene zijdelingsche beweging mede; deze stooten behooren echter ook hier niet tot die, welke eene berekening toelaten, of waarvan de uitwerking zich laat vooruitbepalen. In de voortgaande beweging brengen dus deze stooten, de zijstooten, geene verandering, maar wel is dit het geval bij de draaijing.
Gaat men toch na, wat er gebeurt bij het stooten van den bal in eenig punt C, buiten de loodregte middellijn XX', dan is het ligt te begrijpen, dat daardoor eene draaijing ontstaat rondom eene as, die loodregt staat op de lijn CM, die het geraakte punt met het middelpunt verbindt. Wanneer men zich nu uit de beginselen van de leer der beweging herinnert, dat de draaijing rondom eene as zich evenzeer—en op de zelfde wijze als vroeger bleek het geval te zijn met twee krachten, die op een zelfde punt werkten,—laat ontbinden in twee andere draaijingen rondom gegevene assen, en dat zich altijd omgekeerd uit twee draaijingen eene enkele laat zamenstellen rondom eene, door constructie of berekening te bepalen, as,—dan ziet men, dat ook hier elke draaijing kan worden ontbonden in twee andere, waarvan de eene plaats heeft rondom de horizontale as YY', die loodregt staat op de rigting der voortgaande beweging, en die dus in denzelfden of juist tegengestelden zin geschiedt als de draaijing, die door de wrijving ontstaat (en dat wel naarmate C boven of onder de horizontale middellijn YY' ligt),—terwijl de andere wenteling die middellijn van den bal tot as heeft, die loodregt op het vlak van de tafel staat. Eigenlijk zoude er bij die ontbinding in het algemeen [ 87 ]nog eene derde draaijing ontstaan, en wel rondom eene horizontale middellijn als as, volgens de rigting der beweging gelegen: deze kan echter wegens de wrijving slechts eene geringe uitwerking hebben, en wij zullen ze hier buiten rekening laten. Wanneer men nu de betrekkelijke snelheden van omwenteling voorstelt door de lengte der loodlijn op de as van draaijing, (hetgeen uit de leer der beweging volgt), zoo laat het hier gezegde eene zeer aanschouwelijke voorstelling toe.
Men stelle daartoe, dat de rigting der Queue het vlak, dat loodregt op de rigting der beweging staat, in eenig punt C treffe, en vereenige dit met het middelpunt, dan is deze juist de genoemde loodlijn op de as van draaijing en kan, naar het straks gezegde, tevens als maat van de rotatie-snelheid gelden: zij stelt dus eene soort van maat van die draaijing in rigting en in grootte tevens voor. Deze MC ontbinde men, volgens het parallelogram van krachten, in twee andere MA en MB, volgens de onderling loodregte middellijnen XX' en YY', waarvan de eerste verticaal, de tweede horizontaal is getrokken; dan is de verticale lijn MA de overeenkomstige maat der draaijing rondom de horizontale as YY', waarop zij loodregt staat; en evenzoo bepaalt de horizontale lijn MB de draaijing rondom de verticale as YY'. Bij nadere beschouwing volgt dan tevens, dat de draaijing door MA voorgesteld geheel dezelfde is als die welke een stoot door A zoude te weeg brengen: terwijl op dezelfde wijze door eenen stoot door B eene draaijing zoude te weeg worden gebragt, die juist dezelfde is als die, welke door MB als maat wordt voorgesteld. De stoot door C heeft dus geene andere uitwerking dan twee gelijktijdige stooten door A en B te zamen zouden gehad hebben.
De eerste draaijing, door MA voorgesteld, valt dus te zamen met die, door de wrijving teweeggebragt, en is in denzelfden zin, dus positief, als A boven,—in tegengestelden zin, dus negatief, als A beneden het middelpunt M ligt. Wat de draaijing om de verticale as XX' aanbelangt, die door MB is voorgesteld, deze is van links naar regts als B ter linker zijde van M ligt: bevond B zich aan de regterzijde van het middelpunt, dan zoude de draaijing van regts naar links plaats hebben. De plaats van het punt C, in zoo verre daarvan de betrekkelijke ligging van de punten A en B ten opzigte van het middelpunt M afhangt, bepaalt [ 88 ]dus de overeenkomstige draaijingen om de horizontale en verticale as. Ligt C in de lijn XX', zoo is BM en daarmede de draaijing om eene verticale as nul: men heeft het vroeger beschouwde geval terug. Is C daarentegen op YY' gelegen, zoo heeft omgekeerd de stoot geene draaijing om de horizontale as, maar slechts eene om de verticale as ten gevolge. En evenzoo, als C tusschen de assen XX' en YY' ligt, zal de draaijing om eene verticale as toenemen, naarmate C zich tuin de eene of andere zijde van XX' verder van die lijn verwijdert: maar naar diezelfde mate neemt dan ook, bij gelijken afstand tot het punt M, de draaijing om eene horizontale as af. Deze draaijing neemt wederom toe, naarmate C zich in het algemeen verder van YY' verwijdert; terwijl alsdan, wanneer de afstand tot het middelpunt dezelfde blijft, de draaijing om de verticale as al kleiner en kleiner wordt. In het algemeen zal de draaijing voor eenen stoot van gegeven kracht toenemen, naarmate C zich verder van het middelpunt verwijdert.
Dit moge genoeg zijn omtrent de verklaring van den invloed, dien een zijstoot op de draaijings-bewegingen van eenen bal uitoefent: wij kunnen nu in het algemeen wel nagaan, welke verschillende verschijnsels er moeten te weeg gebragt worden, ten gevolge van de verschillende plaatsen van het punt C met betrekking tot den eindbaan van den handbal, wanneer deze den speelbal of den band heeft geschokt. Daartoe heeft men slechts de draaijing telkens naar het bovengezegde in twee andere draaijingen te ontbinden, waarvan die om de horizontale as hier wel den meesten invloed uitoefent, en dus voornamelijk in aanmerking komt. Naarmate zij met de uitwerking van de wrijving in gelijken of tegengestelden zin valt, zal de handbal zich volgens parabolen bewegen, waarvan de bogt zal afhangen van de betrekkelijke kracht dier beide draaijingen. De nu nog plaats hebbende draaijing om de verticale as zal, om het zoo eens uit te drukken, eene verbetering aan die parabool aanbrengen, en wel in denzelfden zin als het punt B ten opzigte van M ligt. Werd de handbal b.v. in Fig. 9—13 links van het middelpunt geraakt, dan zullen alle daar beschreven parabolen iets naar de linkerhand afwijken. Wij willen ons hierbij echter niet ophouden, maar liever nu een paar voorbeelden geven van den [ 89 ]schok van den handbal tegen den band, naarmate hij hoog of laag en daarbij regts of links gestooten werd. In Fig. 17 is de handbal, zoo
als de nevenstaande figuur aanduidt, laag, in Fig. 18 daarentegen hoog geraakt. Bij iedere figuur zijn vier rigtingen beschouwd, langs welke de handbal den band schokt: eene daarvan (met 4 geteekend) is loodregt op dien band: de andere zijn met 3, 2 en 1 aangeduid, naarmate zij 3⁄4, 2⁄4 of 1⁄4 van eenen regten hoek met dien band vormen. De invallende rigtingen liggen alle regts in de figuur: de teruggekaatste komen dus in de linker helft, en daarbij zijn zij met dezelfde nommers voorzien als de rigtingen van inval, waartoe zij respectievelijk behooren. De uitwerking verder van eenen zijstoot ter regterzijde van het middelpunt is met één streepje aangeduid, terwijl twee streepjes beteekent dat de bal links is gestooten. De snelheid van den bal vóór den schok is 3 meters per seconde. De aandachtige beschouwing dezer figuren, voor twee bijzondere en genoegzaam verschillende gevallen, zal het boven gezegde kunnen bevestigen en zoo noodig verduidelijken. Slechts moge hierbij nog ter loops worden aangemerkt, dat er soms [ 90 ]gevallen kuunen voorkomen, dat de parabool, door eenen zijstoot te weeg gebragt, de oorspronkelijke parabool,—waarbij de stoot niet bezijden de loodregte middellijn, maar even hoog boven de tafel is aangebragt,—in haren loop snijdt. Hiervan diene tot voorbeeld Fig. 18, stoot 2; was de bal door eenen regter zijstoot voortgestuwd, zoo beschrijft hij de parabool 2', die wel, uit den bal gezien, eerst ter regterzijde van de eerste afwijkt, maar deze naderhand wederom snijdt, om verder ter linkerzijde te blijven voortgaan.
Uit de theorie leeren wij verder omtrent de draaijing rondom eene verticale as, dat zij het sterkst is, wanneer de bal geraakt wordt op de helft van den straal, ter regter- of linkerzijde van het middelpunt, naarmate de draaijing van regts naar links of van links naar regts moet wezen; voor eenen sterken stoot van 7 meters wordt alsdan de snelheid van den bal 51⁄4 meters, terwijl deze 33⁄5 meters bedraagt voor eenen gewonen stoot van 5 meters. Gedurende den loop van den bal in eene kromme lijn zal het gedurig werken der wrijving ten gevolge hebben, dat de oorspronkelijke draaijing van den bal zich alzoo met die der wrijving te zamen stelt, dat de eindresultante eene draaijing wordt om eene as, die in het vlak ligt, dat loodregt op de eindbeweging staat. In het algemeen zal de zijstoot de vermeerdering van het effect ten gevolge hebben, dat is van de beweging, die er na eenen tweeden schok overblijft.
Omtrent de kromme lijnen zelve zal er daarbij een maximum ontstaan, wanneer zoowel de hoek van de gemeenschappelijke raaklijn tusschen den handbal en den speelbal, als ook de afstand van het punt, waar de schok wordt aangebragt, tot de eindrigting het grootste wordt. Was de handbal bij den schok in zijnen eindtoestand, dan is de kromme lijn van de beweging na den stoot eene grootste, wanneer hij den speelbal snijdt, dat is slechts even aanraakt: alsdan maakt de raaklijn van de kromme lijn, dat is de rigting van het begin der kromlijnige beweging, met de oorspronkelijke rigting eenen hoek van 33°, wanneer men eenen stoot van 7 meters onderstelt; en dan is ook de eindrigting van de loopbaan des handbals 1⁄4 meter van het punt verwijderd, waar de schok heeft plaats gevonden. Was de handbal zoo laag mogelijk geraakt, zoo moet men, om de maximum kromme lijn te [ 91 ]verkrijgen, den speelbal bijna geheel vol raken, dat is zoodanig, dat de verbindingslijn der middelpunten slechts weinig van de rigting van den handbal vóór de botsing verschilt; alsdan is voor stooten van 7 en 5 meters het punt, waar de schok plaats grijpt, 9⁄10 en 7⁄30 meter respectievelijk van de eindrigting verwijderd.
Wij beschouwden hier slechts de uitwerking van alle horizontale stooten op den handbal voor en na de botsing tegen den speelbal en tegen den band, terwijl wij de beweging van dien speelbal steeds langs de regte lijn zagen plaats vinden, die de middelpunten der ballen verbindt. Daaruit volgt dus van zelf, hoe men stooten moet om den speelbal eene bepaalde rigting te geven, bijv. om dien te maken; maar er is een ander spel, van vrij wat meer belangrijkheid, waarbij dan de handbal twee speelballen na elkander moet aanraken, het caramboleren. Hier komt het er dus op aan, om den handbal na den schok met den eersten speelbal zulk eene rigting te geven, dat hij den tweeden raakt, somtijds na tusschentijds één of meermalen den band te hebben geraakt; en hiertoe dient voornamelijk het raken van den handbal in verschillende punten, waardoor deze dan ook na den schok met den eersten speelbal telkens eenen anderen loop verkrijgt. Zijn nu in het algemeen de hier verklaarde beginselen genoegzaam om de verschillende uitgevoerde caramboles te verklaren, er is echter nog eene geheel andere soort van stooten, die weder verschillende uitkomsten oplevert, maar die dan ook alleen door geoefende spelers kan worden uitgevoerd,—die stooten namelijk, waarbij de Queue niet meer horizontaal wordt gehouden, maar in eene meer of minder hellende rigting wordt gebragt.
Hierbij doet zich weder een nieuw verschijnsel op, namelijk de schok tusschen de tafel en den bal, die onmiddellijk volgt op den schok tusschen den bal en de Queue. Zoolang nu de rigting der Queue door het middelpunt van den bal gaat, heeft deze stoot slechts invloed op de snelheid der voortgaande en draaijende beweging; maar zoodra de rigting van den stoot niet meer door het middelpunt gaat, beschrijft de bal eene kromme lijn,—daar alsdan de wrijving niet meer in dezelfde [ 92 ]rigting werkt als die, waarin de bal voortgaat, zoodat hier de toestand van den bal na den stoot, in dit opzigt, eenige overeenkomst heeft met dien van eenen bal, die horizontaal is voortgestooten, en daarna tegen den speelbal of tegen den band eene botsing heeft ondergaan. De kromming dier kromme lijn, hier mede eene parabool,—en wel om dezelfde reden als boven,—zal hare bolle zijde vertoonen naar den kant, waar de hellende stoot is aangebragt; de bal zal dan regts of links van de regte lijn afwijken, naarmate hij links of regts geraakt is. Om de eindrigting te bepalen, heeft men slechts de rigting der Queue tot aan de tafel te verlengen, en dit punt met het steunpunt van den bal te vereenigen, dan zal de eindrigting van den bal aan deze lijn evenwijdig loopen.
Daaruit volgt dan ook, dat een aldus door eene hellende Queue geraakte bal eindelijk zoude terugloopen, wanneer slechts het punt, waar de Queue verlengd zijnde op de tafel zoude komen, digter bij den speler was gelegen, dan het steunpunt van den bal. In de praktijk bestaat hierbij de groote zwarigheid, die er in gelegen is, om dadelijk na den schok alle gemeenschap tusschen Queue en bal te doen ophouden. En dit is hier veel moeijelijker dan vroeger; daar toch was de snelheid van den bal grooter dan die van de Queue, de bal ontliep als het ware de Queue: hier daarentegen is in het algemeen de snelheid van den bal kleiner dan die van de Queue, en moet derhalve de Queue dadelijk na den schok snel worden teruggetrokken, wil men den bal niet in zijnen loop terughouden, of althans verstoren. Slechts zeer goede spelers zijn dus tot deze stooten in staat. Dit was het groote kunststuk van mingaud, die eenen handbal, zonder speelbal of band aan te raken, in het midden zijner beweging deed terugkeeren, stil liggen of eenen cirkel beschrijven. Hij bragt dit verschijnsel te weeg door den hellenden stoot, die eerst mogelijk is geworden, sedert hij de Queue met eene pommerance voorzag.
- ↑ In deze en vele volgende figuren is behalve de rigting, die de ballen moeten doorloopen, in eene tweede figuur aangegeven, hoe de stoot moet gegeven worden, om die uitkomsten te weeg te brengen. Zoo is hier in de tweede figuur eene doorsnede van den bal geteekend, loodregt op de tafel en tevens loodregt op de rigting van den stoot. Om den bal nu volgens H 2 te doen loopen, moet men hem zeer hoog raken, volgens den stoot 2 in die tweede, figuur. Wil men den bal daarentegen de kromme H 3 doen beschrijven, zoo is een zeer lage stoot, in de tweede figuur door 3 aangeduid, noodzakelijk. In het algemeen zijn in de eerste figuur de rigtingen en in de tweede de daartoe behoorende stooten met dezelfde nummers voorzien.